Presidential names – popularity predictions

One year ago I wrote this where I used the 1000 most popular baby names each year to find spikes in name popularity. Inspired by this here (or maybe by stealing her idea), I connected these spikes to real or fictional characters in history.

Somehow I missed that the social security administration allows researchers to download more complete data, data which includes ALL names (almost – there must be at least 5 people given the name). Further, it’s conveniently accessible here, so let’s do more investigation. Rather than pull out names with extreme properties as before, let’s try to predict changes in a subset of names. There were some spikes in popularity for a couple presidential names in our last look (specifically for Woodrow and Grover), so do these spikes occur with most presidents’ names? If so, can we predict how big the swing in popularity will be? Turns out, yes and yes.

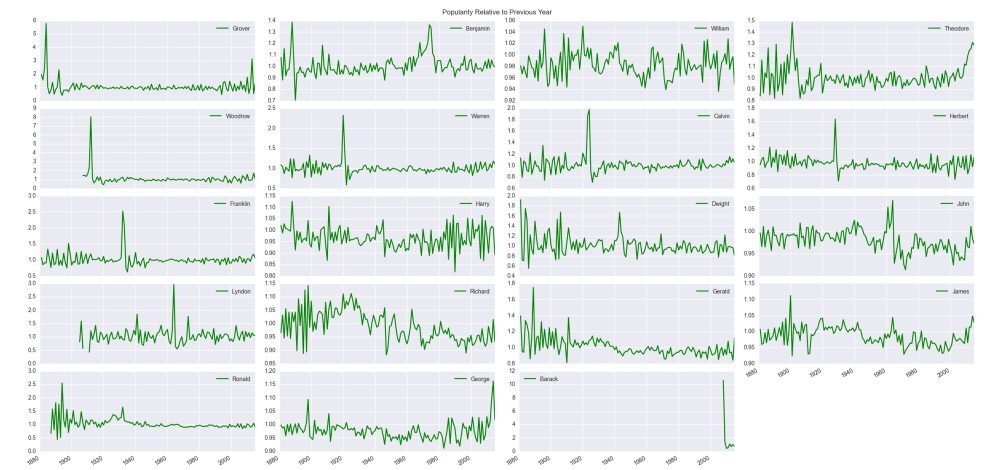
rr_all — For each president’s name (no repeat images if multiple presidents had the same name), we take the percentage of babies born with that name in each year. Taking ratios of this value over the previous year, this shows how the popularity of that name is changing. For most names, the max or at least a kind of local max, occurs in the year before a president takes office (election year). So, if we know a presidential candidate’s name, can we predict the size of this popularity swing (assuming they are the candidate elected to be president) using only the data prior to the election year?

We will essentially perform a least squares regression (see this for a some technical stuff concerning stats language vs linear algebra), but before we get to modeling “presidential popularity,” let’s take a cursory look at the data. I have the first names and the number of babies given those names each year from 1880 to 2015 (for security reasons, there had to have been at lease 5 babies with that name). As the total number of babies born each year varies, we normalize by taking the percentages of babies born with a particular name each year. Not surprisingly the variety of names has changed drastically over time. There were about 1,000 unique names given in 1880 compared with about 14,000 in 2015. With the number of unique names trending upward, the percentage of babies born with historically traditional names has generally decreased.

Variety of names increasing

Percentage of babies with a given name correspondingly decreasing

The clear downward trends on the right are your “Williams,” “Georges,” “Richards” – the more common names. Still, there are clearly years where these names reverse their general trends. As our goal will be to predict the popularity of a presidential name in an election year or slightly post election year, maybe this is the value we should predict – the percentages of babies born with the presidential candidate’s name. There is a problem with scale. For example, “Barack” had a huge spike in popularity during and after his campaign, but the percentage was orders of magnitude smaller than most other names (at its highest less than 0.0004 compared to a name like “William” which is around 0.01 at its least popular level). The trends of big names would dominate, and the model would essentially say “do what the most common names do.” Further, these common names tend not to vary much from their general long-term trends, so we need to find some other measure to predict. Instead of the percentage of babies born, we will use relative risk. For a given name, say $x$ and year $y$ let $x_y$ be the percentage of babies born in $y$ with name $x$ . Then the relative risk associated with name $x$ in $y$ is $x_{y}/x_{y-1}$ . The term relative risk is often used in epidemiology but is relevant here if we interpret it as the risk of being named $x$ in year $y$ relative to year $y-1$ . This has the benefit of being a very localized measure and accounts for the previously mentioned scale issue. I am going to use the term “relative popularity” in place of relative risk just because I think this better describes what we are doing (even though relative risk is a well defined concept). We will try to predict spikes in relative popularity for presidential names, considering only the first time the president runs for office. We will not examine relative popularity if or when a president runs for re-election.

While relative popularity is probably our best option, it does accentuate less common names (it doesn’t take much change to make this value large when your denominator is tiny). For the heck of it, now that I had a bigger data set, I wanted to see what name had the largest relative popularity from the full set. This was “Omarion,” (popularity due to debut of R&B singer Omari Ishmael Grandberry in B2K) whose relative popularity jumped as high 83, but this represents a jump from the minuscule 0.000003 in 2001 to the still very tiny 0.000249 in 2002. All this means to me is that our model should include the current popularity of a name (percentage of babies born with that name) as a predictor. By the way, even though we will be predicting relative popularity which is calculated based on these percentages, and we will also be using name percentages as a predictor, this is not cheating. The model will only see percentages prior to those used in calculating relative popularity. I’ll explain the model more fully below.

Another reasonable predictor would be previous relative popularity (if a name was already gaining or losing popularity, that trend may continue). You will notice that there is quite a bit of noise/variability in relative popularity, so I will smooth the data. Specifically, for each year, I’ll average this value with the previous 4 years. I’ll do the same for the name percentages data. This is common in signal processing.

George — Top: Relative popularity for “John.” Bottom: Relative popularity smoothed by averaging each year with the previous 4 years. By the way, the two largest spikes in the non-smoothed data probably relate to his election and then his assassination.

So let’s do a simple ordinary least squares regression with just these two predictors. We will fit $y = \beta_0 + \beta_1x_1 + \beta_2 x_2 +\epsilon$ where

$y$ is the maximum relative popularity of a president’s name from his election year through his last year in office. This value usually spikes in the election year, but not always – this range should cover the potential influence of the president’s name.
$x_1$ is the name’s popularity (percentage of babies given the president’s name) from the year before the election year (smoothed)
$x_2$ is the relative popularity for the president’s name from the year before the election year (also smoothed)

Note we are predicting the spike in relative popularity without using any “future data” meaning we are using only data before the election year. Turns out, this is not a great model. It seems reasonable that once a name achieves a certain level of commonality, continuing to increase its popularity may not matter much. So instead of a linear relationship with $x_1$ , lets replace $x_1$ with $\ln (x_1)$ as a predictor. This fits the data better than I expected ( $R^2 = 0.75$ ), and is represented in the image below.

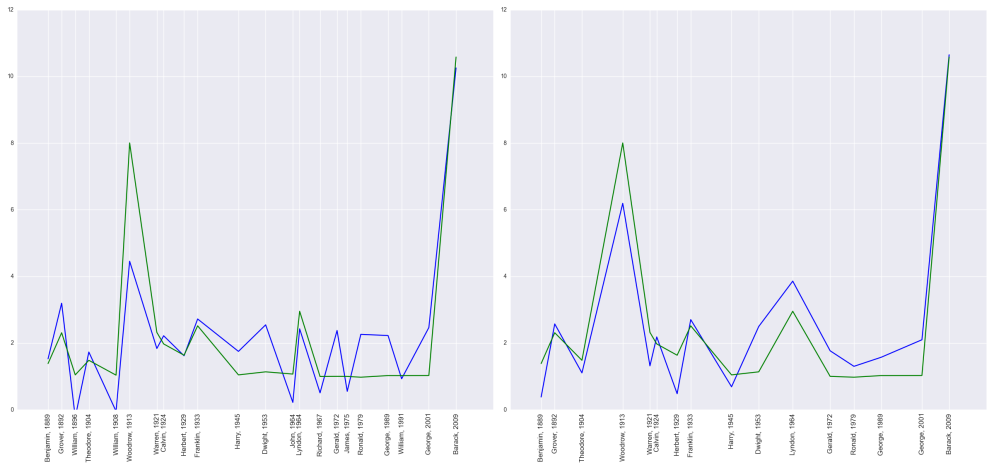
regression_1 — Green: actual max relative popularity of presidential name from election year though end of their first term. Blue: predicted max relative popularity. Left: model run on all presidential names after 1885. Right: same model fit after removing the most common names. These common names tend to have a relative popularity that remains constant near 1 (no change in name popularity).

Not bad, but there are still some issues to overcome. When we examine the error vs. predicted values, many of these points lie along a straight line meaning for many presidents, the error is proportional to the predicted value. The model is useless for these presidents; this corresponds to the names in the figure above whose value is near $1$ (indicates no change in name popularity) while the blue prediction varies around it. By inspection, the names that show no change in popularity tend to be more common names (“George,” “William,” “James,” etc…). Although I tried to account for this by including (the $\ln$ of) name popularity in my model, evidently when names get very popular, you may as well just assign a relative popularity of $1$ . I’ll end up setting a switch so that if a name is very popular, the model will predict a relative popularity of $1$ , and we will fit the same model to the remaining names. We will fit our model to presidential names where the percentage of babies born with that name around the election year is less than $0.01$ . This removes “William,” “John,” “Richard,” and “James,” and we are left with 16 data points to fit our model. The resulting model ( $R^2 = 0.77$ ) has better looking residuals when plotted against predicted values, but another issue is present.

Notice the predicted values tend to estimate too low for early presidents and too high for later presidents. This indicates there is a time factor that needs to be considered. Maybe the names of more recent presidents don’t have as much influence on baby names as in the past. The easiest way to account for this is to add time as a predictor. My final model sets $y_i =1$ if the percentage of babies born before the election year is greater than $0.01$ , and then on the remaining $16$ names, we fit the model

$y = \beta_0 + \beta_1x_1 + \beta_2 x_2 + \beta_3 x_3 +\epsilon$

$y$ is the maximum relative popularity of a president’s name from his election year through his last year in office.
$x_1$ is the natural log of the name’s popularity from the year before the election year (smoothed)
$x_2$ is the relative popularity for the president’s name from the year before the election year (also smoothed)
$x_3$ is the index of the name to account for the time component of the series.

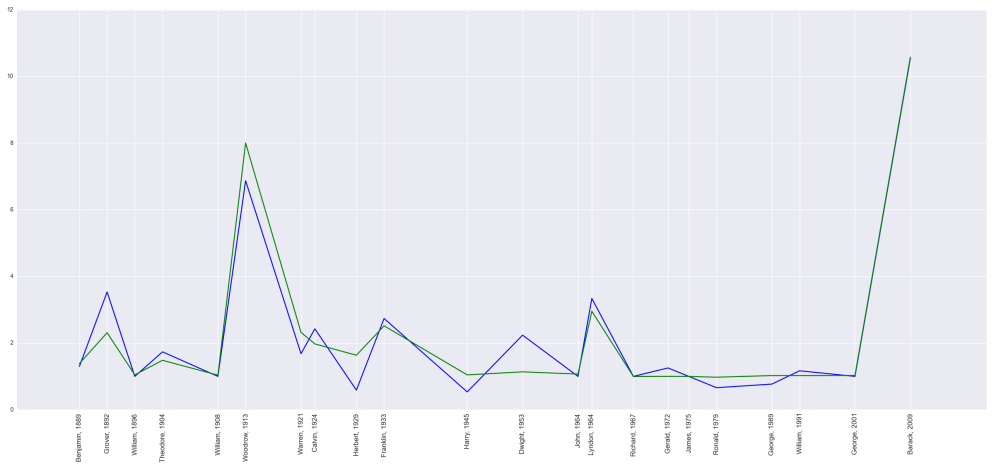
regression_2 — Final model. Green: actual max relative popularity of presidential name from election year through the end of their first term. Blue: predicted max relative popularity. Note: “Dwight” spiked in popularity during WWII (when he was the Allied Supreme Commander) prior to his bid for presidency which may explain why our prediction overestimated his change in popularity.

This obviously isn’t a linear model since we’ve instituted a switch that sets our predicted value as $1$ or turns to the fitted model, but the fitted portion has a crazy-high $R^2 = 0.94$ (adjusted $R^2 = 0.93$ ), and there appears to be no issues with our residuals. This almost seems too good, and we do have to be careful if we fit many models or cherry-pick our data. As we consider more models, we are more likely to have one fit purely by chance. Still, given the simplicity of our model and that the presence of these predictors make intuitive sense, I don’t think this is an issue; we seem to have a good model.

Two questions remain. Do the parameter estimates make sense, and is the model useful for predictions? There does not appear to be an issue with multicollinearity, so we should be able to interpret our model parameter estimates. We have $\hat{\beta_0}=12.59,$ $\hat{\beta_1}=-1.50,$ $\hat{\beta_2}=-0.13,$ and $\hat{\beta_3}=-0.14$ , all of which are significant. The intercept term in some sense sets the default change in relative popularity to be around $12$ . Then $\hat{\beta_1}$ will cause the spike to be smaller when the popularity of the name is larger. The term $\hat{\beta_2}$ is somewhat of a surprise. This says the spike in popularity will be smaller when the name was already tending to grow in popularity. I guess a presidential name is better at bringing back a name that was fading in popularity rather than emphasizing a name that was already growing in popularity. Finally, as we suspected, $\hat{\beta_3}$ shows the spike in popularity is reduced for more recent presidents. I guess presidential names aren’t what they used to be.

Finally, to get some idea of how well this will work for prediction, I’ll perform a type of cross-validation. Since I have such a small set of data, I fit the same least squares model multiple times, each time leaving out just a single name. I used the resulting model to predict the left out data point and calculated the error. Doing this for each removed data point and summing the squared error, I can compute the length of a kind of overall error vector. I can compare this to the length of $y$ and obtain a “predicted $R^2$ ” metric. This comes out to be $0.875$ , indicating my model indeed may be useful for prediction.

By the way, the model predicts “Donald” will be $3.10$ times more popular from one year to the next near this election year ( $\pm 1.82$ for a 95% prediction interval) or “Hillary” will be a whopping $6.88$ times more popular ( $\pm 2.02$ ). Of course, several unique aspects may invalidate the model we just found. We didn’t examine girls’ names, and these are two of the least popular and most polarizing presidential candidates in history. We’ll see how the estimate holds up in a couple years….